The nonlinearity problem : Mutlilayer Perceptron [nn part 3]
Hello humans, by now you should know what the heck is a perceptron : a way to find the parameters w and b of a binary linear classifer. Recall that we will be using the following definition of a b.l.c :
\[y = \mathcal{H}(\mathbf{x} \cdot \mathbf{w}-b)\]With a perceptron we can easily find appropriate values of b and w to compute many boolean functions. For example, we can do it easily with the “OR” function :
\[x_1\vee x_2 \text{ also noted } x_1 + x_2\]The “OR” function has the following truth table :
| x1 | x2 | x1 + x2 |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
If we plot these values, we can see that we can separate them by a line :
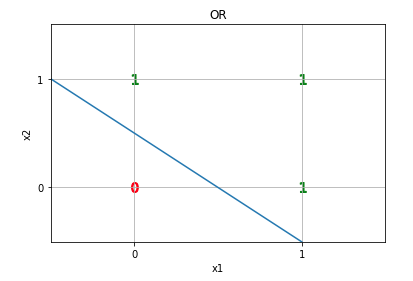
So, we have binary values and they are linearly separable, therefore we can implement this function using a perceptron by setting :
\[\mathbf{w}=\begin{pmatrix}10\\10\end{pmatrix}\text{ and }b= 5 \\ x_1\vee x_2=\mathcal{H}(10\cdot x_1+10\cdot x_2-5)\](Note that we could have used other values). Just to make sure it works, let’s manually compute the result :
| x1 | x2 | 10*x1 + 10*x2 - 5 | H |
|---|---|---|---|
| 1 | 1 | 15 | 1 |
| 1 | 0 | 5 | 1 |
| 0 | 1 | 5 | 1 |
| 0 | 0 | -5 | 0 |
Ok, nice, but what about the XOR function ?
| x1 | x2 | x1 xor x2 |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Try to separate these points by a single line…
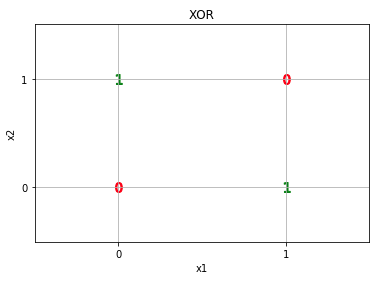
Yep, you can’t. Perceptrons can only classify linearly separable data.
But let’s try to be a little bit smart and go back to the definition of the “Xor” :
\[x_1 \oplus x_2 = (x_1 \wedge \neg x_2) \vee (\neg x_1 \wedge x_2)\]The xor function is made of 3 basic operations : one OR, and two ANDs. The two ANDs are really similar, let’s call them “partial xor”.
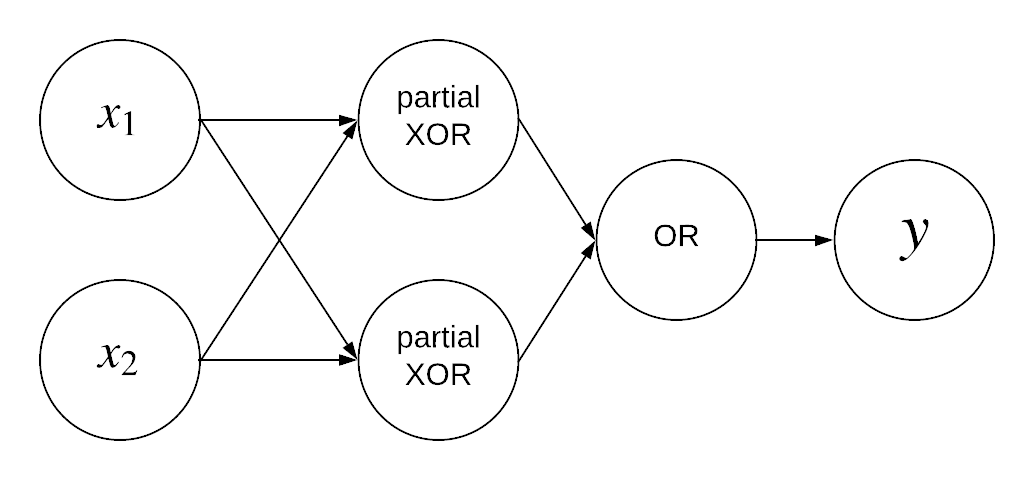
If we focus on one of the partial xor, we can write :
\[\text{Partial xor = }x_1 \wedge \neg x_2\]This function has the following truth table :
| x1 | x2 | x1 Pxor x2 |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
If we plot it, we can see that we can separate the true value from the false by a line.
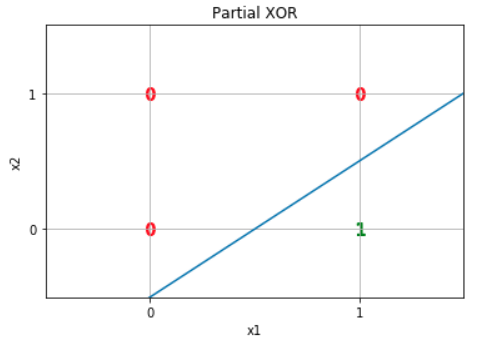
We can use a perceptron, if we set (for example) :
\[\mathbf{w}=\begin{pmatrix}10\\-10\end{pmatrix}\text{ and }b= 5\]If we want to use the same weight vector to implement the second partial xor, we just need to switch the rows of x1 and x2 in x :
\[\mathbf{x}=\begin{pmatrix}x_2\\x_1\end{pmatrix}\]Now that we have a way to represent these 3 operations with perceptrons. We can link them together and build a 2-layer perceptron :
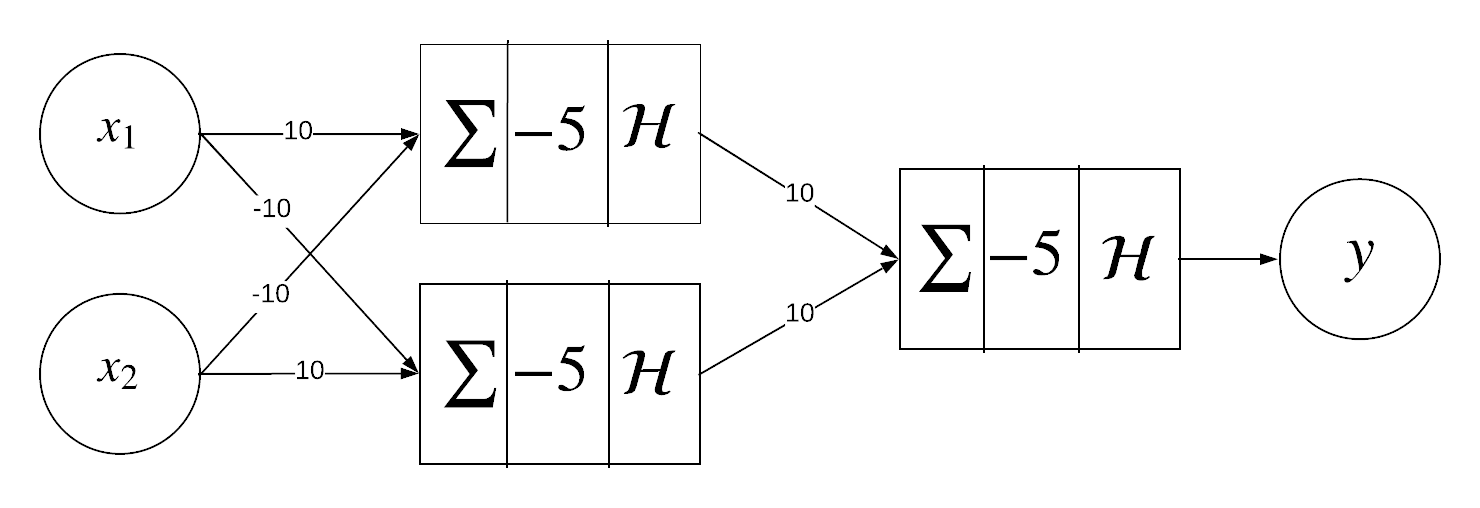
By building a multilayer percetron, we can classify non-linearly separable data.
what’s next
The last 3 articles were just an introduction to the subject of neural networks. They will help us understand what neurons are, how they work, why we use multilayers neural networks.
Let’s gooo